Introduction to tune • tune

Introduction

The tune package helps optimize the modeling process. Users can tag arguments in recipes and model objects for optimization. The search routines in tune can discover these arguments and evaluate candidate values until a combination with good performance is found.

As an example, let’s model the Ames housing data:

library(tidymodels)

data(ames)

set.seed(4595)
data_split <- ames %>%
  mutate(Sale_Price = log10(Sale_Price)) %>%
  initial_split(strata = Sale_Price)
ames_train <- training(data_split)
ames_test  <- testing(data_split)

For simplicity, the sale price of a house will be modeled as a function of its geo-location. These predictors appear to have nonlinear relationships with the outcome:

ames_train %>% 
  dplyr::select(Sale_Price, Longitude, Latitude) %>% 
  tidyr::pivot_longer(cols = c(Longitude, Latitude), 
                      names_to = "predictor", values_to = "value") %>% 
  ggplot(aes(x = value, Sale_Price)) + 
  geom_point(alpha = .2) + 
  geom_smooth(se = FALSE) + 
  facet_wrap(~ predictor, scales = "free_x")
#> `geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs =
#> "cs")'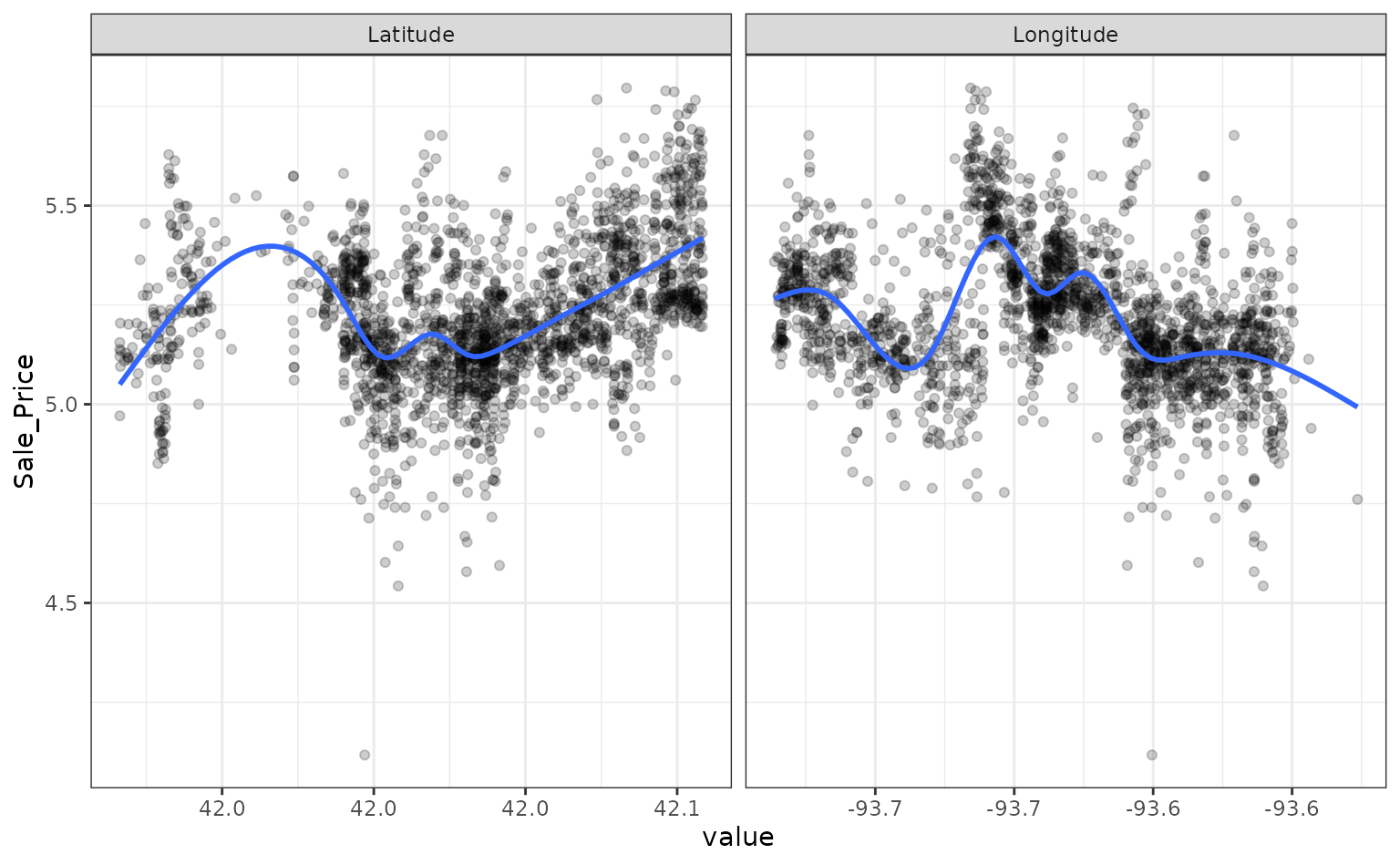

A ggplot2 scatterplot. x axes plot the latitude and longitude, in side-by-side facets, and the log sale price is on the y axis. The clouds of points follow highly non-linear trends, traced by a blue trend line.

These two predictors could be modeled using natural splines in conjunction with a linear model. The amount of “wiggliness” in these splines is determined by the degrees of freedom. An appropriate value of this parameter cannot be analytically determined from the data, so it is a tuning parameter (a.k.a. a hyper-parameter). A common approach is to use resampling to estimate model performance over different values of these parameters and use these results to set reasonable values.

We can tag these parameters for optimization using the tune() function:

ames_rec <- 
  recipe(Sale_Price ~ Gr_Liv_Area + Longitude + Latitude, data = ames_train) %>% 
  step_log(Gr_Liv_Area, base = 10) %>% 
  step_spline_natural(Longitude, Latitude, deg_free = tune())

The package can detect these parameters and optimize them.

However, based on the plot above, the potential amount of non-linearity between the sale price and the predictors might be different. For example, longitude might require more flexibility than latitude. The recipe above would constrain the nonlinearity of the predictors to be the same. We can probably do better than that.

To accomplish this, individual step_spline_natural() terms can be added to the recipe for each predictor. However, we want these to be identifiable; using the same syntax as above, we can’t tell the difference between the two deg_free parameters.

tune() has an option to provide a text annotation so that each tuning parameter has a unique identifier:

ames_rec <- 
  recipe(Sale_Price ~ Gr_Liv_Area + Longitude + Latitude, data = ames_train) %>% 
  step_log(Gr_Liv_Area, base = 10) %>% 
  step_spline_natural(Longitude, deg_free = tune("long df")) %>% 
  step_spline_natural(Latitude,  deg_free = tune("lat df"))

The function extract_parameter_set_dials() can detect and collect the parameters that have been flagged for tuning.

extract_parameter_set_dials(ames_rec)
#> Collection of 2 parameters for tuning
#> 
#>  identifier     type    object
#>     long df deg_free nparam[+]
#>      lat df deg_free nparam[+]
#>

The dials package has default ranges for many parameters. The generic parameter function for deg_free() has a fairly small range:

deg_free()
#> Degrees of Freedom (quantitative)
#> Range: [1, 5]

However, there is a function in dials that is more appropriate for splines:

spline_degree()
#> Spline Degrees of Freedom (quantitative)
#> Range: [1, 10]

The parameter objects can be easily changed using the update() function:

ames_param <- 
  ames_rec %>% 
  extract_parameter_set_dials() %>% 
  update(
    `long df` = spline_degree(), 
    `lat df` = spline_degree()
  )
ames_param
#> Collection of 2 parameters for tuning
#> 
#>  identifier     type    object
#>     long df deg_free nparam[+]
#>      lat df deg_free nparam[+]
#>

Grid Search

Grid search uses a pre-defined set of candidate parameters and evaluates these using resampling. The basic ingredients are:

A grid of candidate values to evaluate.
One or more performance metrics for quantifying how well the model works.
A resampling scheme that can be used to appropriately measure performance (which could be a simple validation set).

To make the grid, a data frame is needed with column names matching the “identifier” column above. There are several functions in dials to created grids (named grid_*()). For example, a space-filling design can be created by:

spline_grid <- grid_max_entropy(ames_param, size = 10)
#> Warning: `grid_max_entropy()` was deprecated in dials 1.3.0.
#> ℹ Please use `grid_space_filling()` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning
#> was generated.
spline_grid
#> # A tibble: 10 × 2
#>    `long df` `lat df`
#>        <int>    <int>
#>  1         6        5
#>  2         7        1
#>  3        10        2
#>  4         3        1
#>  5         1        9
#>  6         9        6
#>  7         1        4
#>  8         3        7
#>  9         9       10
#> 10         5        9

Alternately, expand.grid() also works to create a regular grid:

df_vals <- seq(2, 18, by = 2)
# A regular grid:
spline_grid <- expand.grid(`long df` = df_vals, `lat df` = df_vals)

Note that a 2-degree-of-freedom model is a simple quadratic fit.

There are two other ingredients that are required before tuning.

First is a model specification. Using functions in parsnip, a basic linear model can be used:

lm_mod <- linear_reg() %>% set_engine("lm")

No tuning parameters here.

As mentioned above, a resampling specification is also needed. The Ames data set is large enough to use simple 10-fold cross-validation:

set.seed(2453)
cv_splits <- vfold_cv(ames_train, v = 10, strata = Sale_Price)

The root mean squared error will be used to measure performance (and this is the default for regression problems).

Using these objects, tune_grid() can be used¹:

ames_res <- tune_grid(lm_mod, ames_rec, resamples = cv_splits, grid = spline_grid)
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.

The object is similar to the rsample object but with one or more extra columns:

ames_res
#> # Tuning results
#> # 10-fold cross-validation using stratification 
#> # A tibble: 10 × 4
#>    splits             id     .metrics           .notes          
#>    <list>             <chr>  <list>             <list>          
#>  1 <split [1976/221]> Fold01 <tibble [162 × 6]> <tibble [0 × 4]>
#>  2 <split [1976/221]> Fold02 <tibble [162 × 6]> <tibble [0 × 4]>
#>  3 <split [1976/221]> Fold03 <tibble [162 × 6]> <tibble [0 × 4]>
#>  4 <split [1976/221]> Fold04 <tibble [162 × 6]> <tibble [0 × 4]>
#>  5 <split [1977/220]> Fold05 <tibble [162 × 6]> <tibble [0 × 4]>
#>  6 <split [1977/220]> Fold06 <tibble [162 × 6]> <tibble [0 × 4]>
#>  7 <split [1978/219]> Fold07 <tibble [162 × 6]> <tibble [0 × 4]>
#>  8 <split [1978/219]> Fold08 <tibble [162 × 6]> <tibble [0 × 4]>
#>  9 <split [1979/218]> Fold09 <tibble [162 × 6]> <tibble [0 × 4]>
#> 10 <split [1980/217]> Fold10 <tibble [162 × 6]> <tibble [0 × 4]>

The .metrics column has all of the holdout performance estimates² for each parameter combination:

ames_res$.metrics[[1]]
#> # A tibble: 162 × 6
#>    `long df` `lat df` .metric .estimator .estimate .config             
#>        <dbl>    <dbl> <chr>   <chr>          <dbl> <chr>               
#>  1         2        2 rmse    standard      0.0985 Preprocessor01_Mode…
#>  2         2        2 rsq     standard      0.683  Preprocessor01_Mode…
#>  3         2        4 rmse    standard      0.0970 Preprocessor02_Mode…
#>  4         2        4 rsq     standard      0.693  Preprocessor02_Mode…
#>  5         2        6 rmse    standard      0.0959 Preprocessor03_Mode…
#>  6         2        6 rsq     standard      0.702  Preprocessor03_Mode…
#>  7         2        8 rmse    standard      0.0925 Preprocessor04_Mode…
#>  8         2        8 rsq     standard      0.724  Preprocessor04_Mode…
#>  9         2       10 rmse    standard      0.0918 Preprocessor05_Mode…
#> 10         2       10 rsq     standard      0.728  Preprocessor05_Mode…
#> # ℹ 152 more rows

To get the average metric value for each parameter combination, collect_metrics() can be put to use:

estimates <- collect_metrics(ames_res)
estimates
#> # A tibble: 162 × 8
#>    `long df` `lat df` .metric .estimator   mean     n std_err .config  
#>        <dbl>    <dbl> <chr>   <chr>       <dbl> <int>   <dbl> <chr>    
#>  1         2        2 rmse    standard   0.100     10 0.00145 Preproce…
#>  2         2        2 rsq     standard   0.674     10 0.00777 Preproce…
#>  3         2        4 rmse    standard   0.0996    10 0.00137 Preproce…
#>  4         2        4 rsq     standard   0.680     10 0.00675 Preproce…
#>  5         2        6 rmse    standard   0.0987    10 0.00127 Preproce…
#>  6         2        6 rsq     standard   0.686     10 0.00734 Preproce…
#>  7         2        8 rmse    standard   0.0966    10 0.00122 Preproce…
#>  8         2        8 rsq     standard   0.699     10 0.00662 Preproce…
#>  9         2       10 rmse    standard   0.0965    10 0.00117 Preproce…
#> 10         2       10 rsq     standard   0.700     10 0.00661 Preproce…
#> # ℹ 152 more rows

The values in the mean column are the averages of the 10 resamples. The best RMSE values corresponded to:

rmse_vals <- 
  estimates %>% 
  dplyr::filter(.metric == "rmse") %>% 
  arrange(mean)
rmse_vals
#> # A tibble: 81 × 8
#>    `long df` `lat df` .metric .estimator   mean     n std_err .config  
#>        <dbl>    <dbl> <chr>   <chr>       <dbl> <int>   <dbl> <chr>    
#>  1        16       12 rmse    standard   0.0948    10 0.00120 Preproce…
#>  2        18       12 rmse    standard   0.0948    10 0.00121 Preproce…
#>  3        16        8 rmse    standard   0.0949    10 0.00118 Preproce…
#>  4        16       10 rmse    standard   0.0949    10 0.00118 Preproce…
#>  5        16       18 rmse    standard   0.0949    10 0.00119 Preproce…
#>  6        16       16 rmse    standard   0.0949    10 0.00122 Preproce…
#>  7        18       10 rmse    standard   0.0949    10 0.00119 Preproce…
#>  8        18        8 rmse    standard   0.0949    10 0.00119 Preproce…
#>  9        18       18 rmse    standard   0.0950    10 0.00120 Preproce…
#> 10        16       14 rmse    standard   0.0950    10 0.00117 Preproce…
#> # ℹ 71 more rows

Smaller degrees of freedom values correspond to more linear functions, but the grid search indicates that more nonlinearity is better. What was the relationship between these two parameters and RMSE?

autoplot(ames_res, metric = "rmse")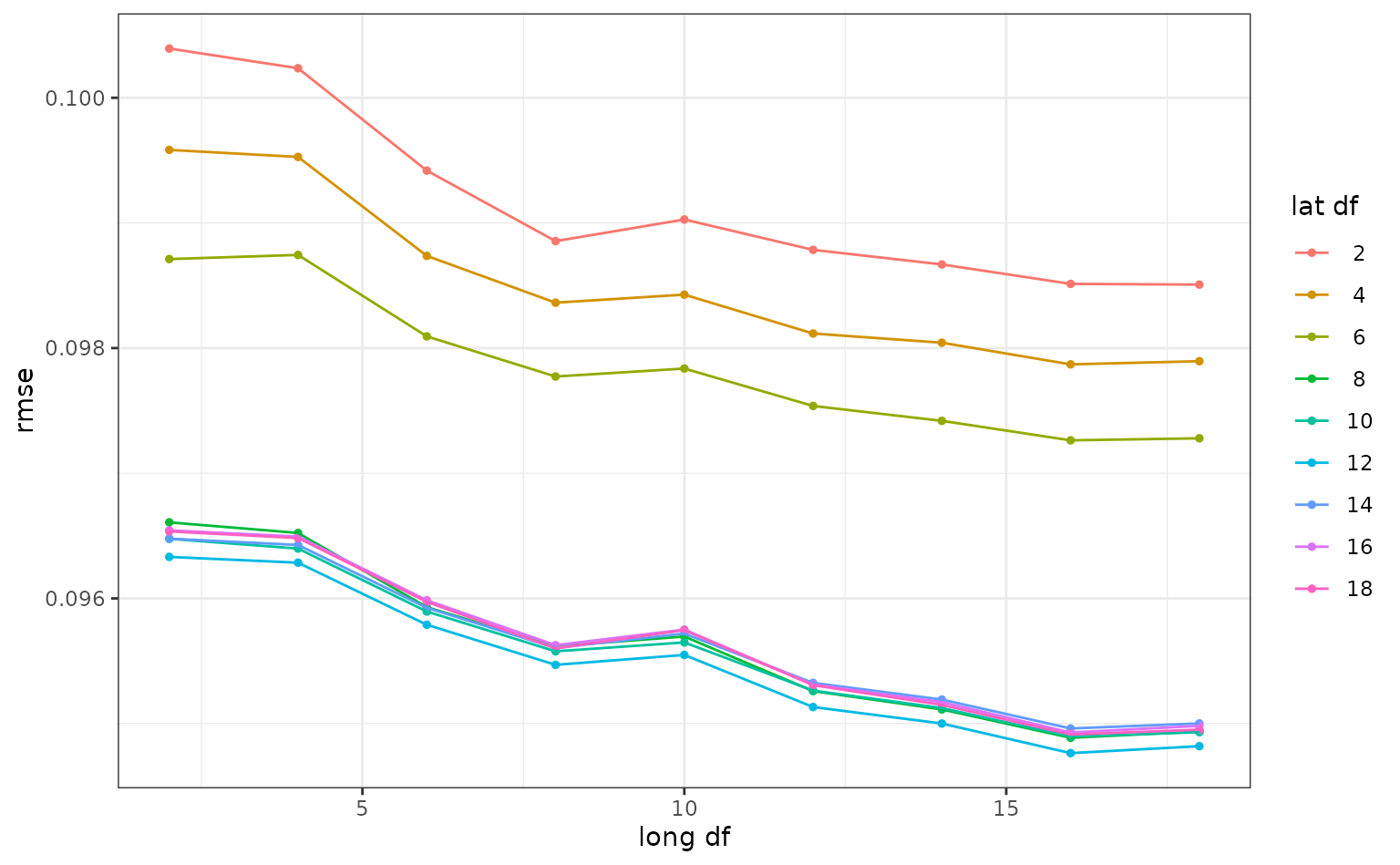

A ggplot2 line plot. The x axis plots the degrees of freedom alotted to the spline parameter mapped to the longitude, and ranges from 0 to 17. The y axis plots the root mean squared error. Lines are colored by the spline terms for the latitude. Generally, from left to right, each line follows a downward trend, and lines from higher latitude degrees of freedom and centered lower.

Interestingly, latitude does not do well with degrees of freedom less than 8. How nonlinear are the optimal degrees of freedom?

Let’s plot these spline functions over the data for both good and bad values of deg_free:

ames_train %>% 
  dplyr::select(Sale_Price, Longitude, Latitude) %>% 
  tidyr::pivot_longer(cols = c(Longitude, Latitude), 
                      names_to = "predictor", values_to = "value") %>% 
  ggplot(aes(x = value, Sale_Price)) + 
  geom_point(alpha = .2) + 
  geom_smooth(se = FALSE, method = lm, formula = y ~ splines::ns(x, df = 3),  col = "red")  + 
  geom_smooth(se = FALSE, method = lm, formula = y ~ splines::ns(x, df = 16)) +
  scale_y_log10() +
  facet_wrap(~ predictor, scales = "free_x")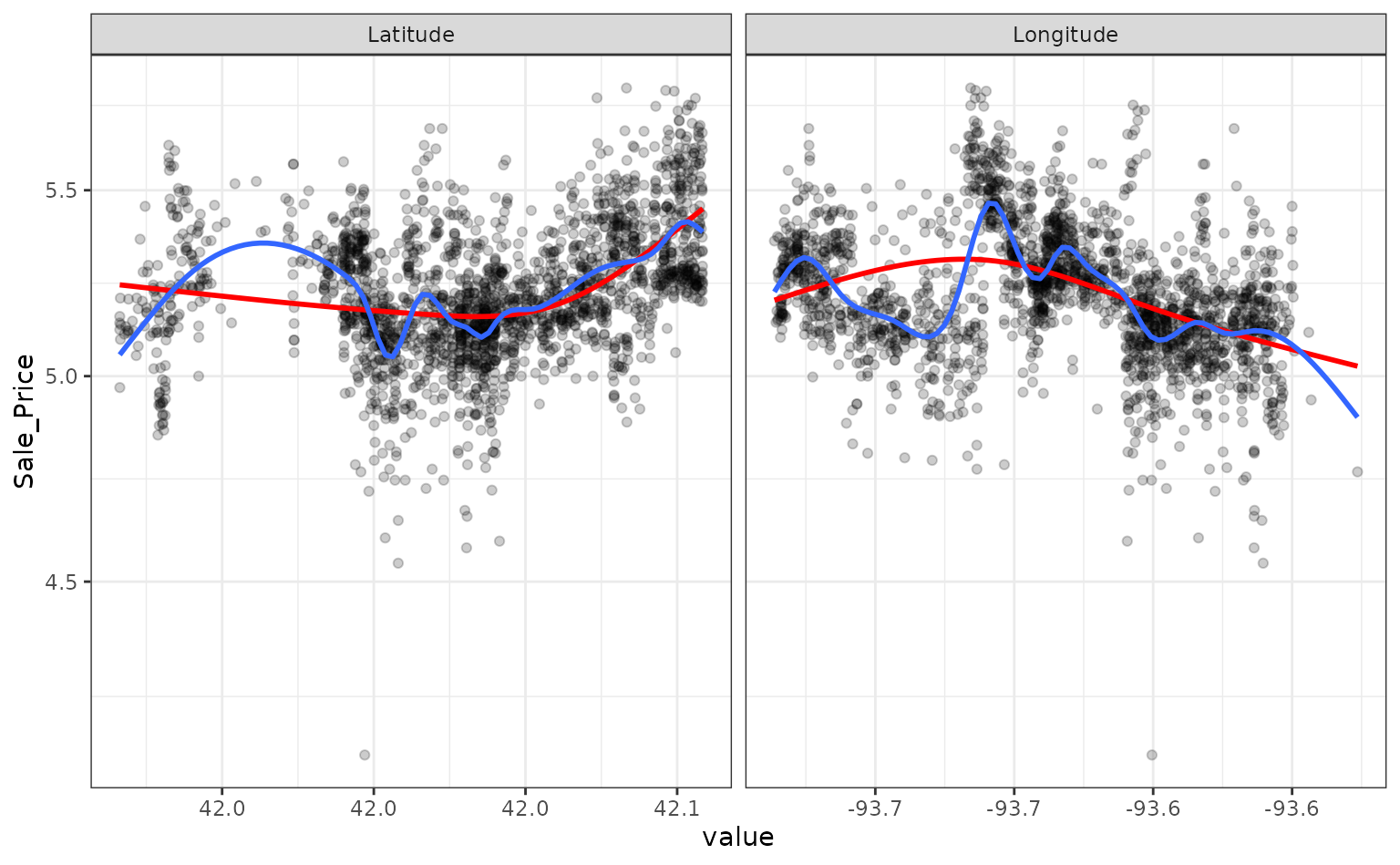

A scatterplot much like the first one, except that a smoother, red line, representing a spline term with fewer degrees of freedom, is also plotted. The red line is much smoother but accounts for the less of the variation shown.

Looking at these plots, the smaller degrees of freedom (red) are clearly under-fitting. Visually, the more complex splines (blue) might indicate that there is overfitting but this would result in poor RMSE values when computed on the hold-out data.

Based on these results, a new recipe would be created with the optimized values (using the entire training set) and this would be combined with a linear model created form the entire training set.

Model Optimization

Instead of a linear regression, a nonlinear model might provide good performance. A K-nearest-neighbor fit will also be optimized. For this example, the number of neighbors and the distance weighting function will be optimized:

# requires the kknn package
knn_mod <- 
  nearest_neighbor(neighbors = tune(), weight_func = tune()) %>% 
  set_engine("kknn") %>% 
  set_mode("regression")

The easiest approach to optimize the pre-processing and model parameters is to bundle these objects into a workflow:

library(workflows)
knn_wflow <- 
  workflow() %>% 
  add_model(knn_mod) %>% 
  add_recipe(ames_rec)

From this, the parameter set can be used to modify the range and values of parameters being optimized³:

knn_param <- 
  knn_wflow %>% 
  extract_parameter_set_dials() %>% 
    update(
    `long df` = spline_degree(c(2, 18)), 
    `lat df` = spline_degree(c(2, 18)),
    neighbors = neighbors(c(3, 50)),
    weight_func = weight_func(values = c("rectangular", "inv", "gaussian", "triangular"))
  )

This parameter collection can be used with the grid functions or with tune_grid() via the param_info argument.

Instead of using grid search, an iterative method called Bayesian optimization can be used. This takes an initial set of results and tries to predict the next tuning parameters to evaluate.

Although no grid is required, the process requires a few additional pieces of information:

A description of the search space. At a minimum, the would consist of ranges for numeric values and a list of values for categorical tuning parameters.
An acquisition function that helps score potential tuning parameter values.
A model for analyzing and making predictions of the best tuning parameter values. A Gaussian Process model is typical and used here.

The code to conduct the search is:

ctrl <- control_bayes(verbose = TRUE)
set.seed(8154)
knn_search <- tune_bayes(knn_wflow, resamples = cv_splits, initial = 5, iter = 20,
                         param_info = knn_param, control = ctrl)
#> 
#> ❯  Generating a set of 5 initial parameter results
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Initialization complete
#> 
#> i Gaussian process model
#> ! The Gaussian process model is being fit using 7 features but only
#>   has 5 data points to do so. This may cause errors or a poor model
#>   fit.
#> ✓ Gaussian process model
#> i Generating 4774 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ! The Gaussian process model is being fit using 7 features but only
#>   has 6 data points to do so. This may cause errors or a poor model
#>   fit.
#> ✓ Gaussian process model
#> i Generating 4770 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ! The Gaussian process model is being fit using 7 features but only
#>   has 7 data points to do so. This may cause errors or a poor model
#>   fit.
#> ✓ Gaussian process model
#> i Generating 4777 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ! The Gaussian process model is being fit using 7 features but only
#>   has 8 data points to do so. This may cause errors or a poor model
#>   fit.
#> ✓ Gaussian process model
#> i Generating 4766 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4786 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4793 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4776 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4771 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4772 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4743 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4751 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4781 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4787 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4791 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4774 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4761 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4783 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4760 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4780 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance
#> i Gaussian process model
#> ✓ Gaussian process model
#> i Generating 4759 candidates
#> i Predicted candidates
#> i Estimating performance
#> Warning: ! tune detected a parallel backend registered with foreach but no
#>   backend registered with future.
#> ℹ Support for parallel processing with foreach was soft-deprecated in
#>   tune 1.2.1.
#> ℹ See ?parallelism (`?tune::parallelism()`) to learn more.
#> ✓ Estimating performance

Visually, the performance gain was:

autoplot(knn_search, type = "performance", metric = "rmse")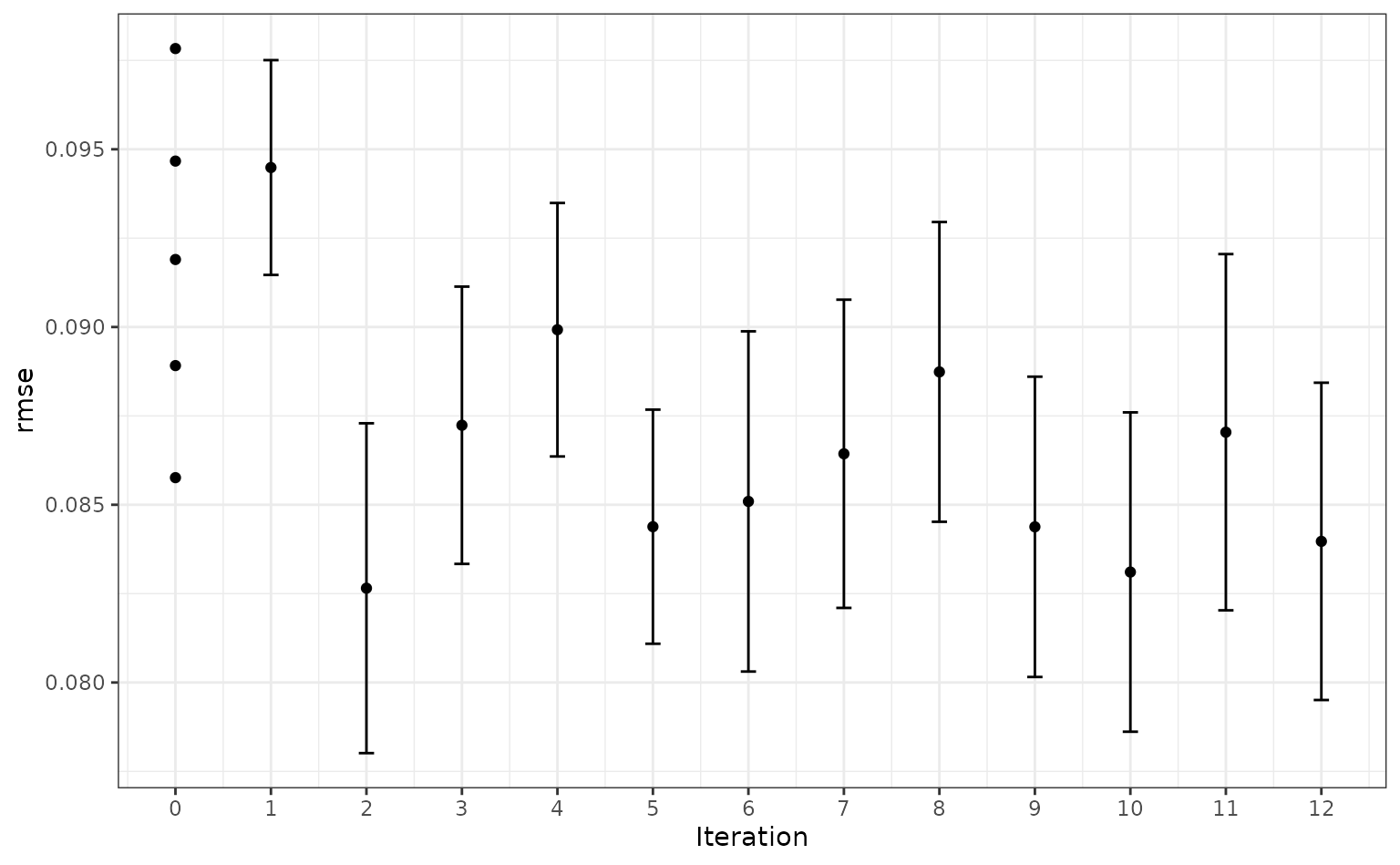

A ggplot2 dot plot. The x axis plots iterations, ranging from 0 to 20, and the y axis plots root mean squared error. After iteration 0, each point has error bars for the metric value. Generally, the error decreases as the iteration increases.

The best results here were:

collect_metrics(knn_search) %>% 
  dplyr::filter(.metric == "rmse") %>% 
  arrange(mean)
#> # A tibble: 25 × 11
#>    neighbors weight_func `long df` `lat df` .metric .estimator   mean
#>        <int> <chr>           <int>    <int> <chr>   <chr>       <dbl>
#>  1         8 inv                 3        4 rmse    standard   0.0812
#>  2         7 inv                 3        4 rmse    standard   0.0813
#>  3         7 inv                 3        3 rmse    standard   0.0814
#>  4         9 inv                 4        5 rmse    standard   0.0815
#>  5         5 inv                 3        4 rmse    standard   0.0819
#>  6        10 inv                 4        6 rmse    standard   0.0821
#>  7         8 inv                 5        4 rmse    standard   0.0822
#>  8        12 inv                 2        4 rmse    standard   0.0826
#>  9        12 inv                 4        2 rmse    standard   0.0828
#> 10         8 inv                 2        6 rmse    standard   0.0829
#> # ℹ 15 more rows
#> # ℹ 4 more variables: n <int>, std_err <dbl>, .config <chr>,
#> #   .iter <int>

With this intrinsically nonlinear model there is less reliance on the nonlinear terms created by the recipe.